Expected Utility Theory#
Imagine you’re offered a choice between $1 guaranteed or $100 with probability \(\frac{1}{80}\) (i.e. with probability \(\frac{79}{80}\), you get $0). Which would you choose?
In game theory, we consider rationality by examining the utility of different outcomes to individuals. To do so, we calculate the expected utility of a set of outcomes, which is the average of the utilities of those outcomes weighted by their probabilities. In the example above, there are two outcomes:
$1 guaranteed. This occurs with probability \(p_1=1\) and we’ll say has utility \(u_1 = 1\).
$100 with probability \(p_2 = \frac{1}{80}\). We’ll say this has utility \(u_2 = 100\).
The expected utility of the first choice would be \(p_1 \cdot u_1 = 1\) because there is only one possible outcome and it has utility 1. The expected utility of the second choice would be \(p_2 \cdot u_2 + (1 - p_2) \cdot 0 = 1.25\) because we obtain utility \(u_2\) with probability \(p_2\) and utility 0 with probability \(1-p_2\). Notice that the expected utility of the second choice is higher! This means that, had you chosen the $1 guaranteed, you would have made the irrational choice, because it is expected that you would get $1.25 with the second choice.
The idea that individuals, when making a gamble, will choose the option that maximizes the expected utility based on their preferences is called the expected utility hypothesis.
Expected Utility#
The expected utility is a calculated value based on two pieces of information: an individual’s preferences for different outcomes and the probability of those outcomes occurring. Let’s illustrate this with an example: Suppose Alice is deciding whether to attend lecture today and her professor is deciding whether to take attendance today. If Alice goes to lecture, she will be bored but get her attendance counted if it’s taken. If she doesn’t, she won’t be bored, but she won’t get her attendance point. We must define the utilities for Alice and her professor in order to construct a payoff matrix.
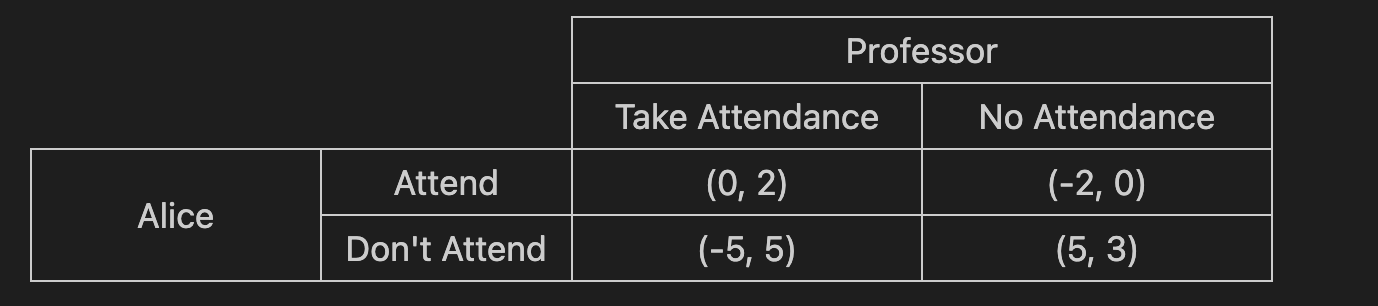
Reading a payoff matrix
A payoff matrix specifies the payoffs of two players. The 2-tuples in each cell define the payoff for both players according to the combination of strategies corresponding to the row and column. For example, the bottom right cell above corresponds to the payoffs for Alice not attending and the professor not taking attendance. The tuples are formatted as (row player, column player), so the first element is Alice’s payoff and the second is the professor’s. The payoff of (5, 0) indicates that that outcome has a utility of 5 for Alice and 0 for the professor.
Let’s say that we know the professor’s strategy: he will take attendance randomly with probability 0.7. Then we can calculate the expected utility of Alice’s two options (attending and not attending) by taking the expected utility of each:
By calculating out Alice’s expected utilities, we see that her utility is maximized by attending, given that the professor’s strategy is to take attendance with probability 0.7.
An important point here is that we rely on the professor’s strategy for playing the game to determine how to maximize Alice’s expected utility. If the professor had a different strategy, then it could be the case that not attending would be the better option.
Let’s formalize our definition of the expected utility.
Definition
The expected utility of a set of \(n\) outcomes \(x_i\) is the average of the utility of each outcome \(u(x_i)\) weighted by the probability of that outcome’s occurrence \(p_i\):
Strategies#
One of the underpinnings of game theory is the idea of strategies, systematic methods of playing games. There are many different ways to conceptualize strategies, some of which we’ve already seen. The professor’s randomness strategy from the last example is one such, maximizing expected utility is another. Strategies tell the players of a game what move to make based on available information, and can be conceived of as a probability distribution over a player’s choices.
There are many different types of strategies. Any strategy that puts probability 1 on a single choice is called a pure strategy; all others are called mixed strategies. If Alice’s strategy had been “never attend class,” this would have been a pure strategy, because the probability of not attending was always 1. The professor’s strategy was a mixed strategy, since there wasn’t a single option with probability 1.


